Skip to content

A short introduction to Mixture-of-Experts (MoE)

panorama city view of Bryggen, Bergen, Norway

Photo by Michael Fousert

Today, I want to talk about something I’ve been discussing a lot lately: Mixture-of-Experts (MoE). It’s a practical way to scale model capacity without paying the full compute cost for every token. Mixtral 8x7B brought this architecture to a lot of people, so we’ll use it as a concrete anchor while we go over how MoE works and what trade-offs it brings.

The release of Mixtral 8x7B

On December 8, 2023, Mistral released Mixtral 8x7B via a magnetic link on X.

Mixtral is a sparse mixture-of-experts model. It has a total of 46.7 billion parameters, but because it only activates a small subset of experts per token, it effectively runs with ~12.9 billion parameters per token.

meme showing a 'Mistral 56B' model blocked by a guardian; the caption says Mixtral is eight 7B experts (Mixtral 8x7B) rather than one 56B model.

The architecture of Mixtral 8x7B is a sparse mixture-of-experts network. It’s a decoder-only model where the feedforward block picks from a set of 8 distinct groups of parameters. At every layer, for every token, a router network chooses two of these groups (the “experts”) to process the token and combine their outputs.

Mixtral uses top-2 routing (num_experts_per_tok: 2), so it’s better described as a sparsely-gated MoE / top‑k routing model. By contrast, Switch Transformer routes to a single expert per token (top‑1). (See: Switch Transformers.)

{
  "dim": 4096,
  "n_layers": 32,
  "head_dim": 128,
  "hidden_dim": 14336,
  "n_heads": 32,
  "n_kv_heads": 8,
  "norm_eps": 1e-5,
  "vocab_size": 32000,
  "moe": {
    "num_experts_per_tok": 2,
    "num_experts": 8
  }
}

The key point is the compute/memory trade-off: sparse routing reduces compute per token because only k experts run per token, but the memory footprint still includes all experts (and routing can add overhead in distributed setups).

Defining MoE

At a high level, a Mixture-of-Experts (MoE) layer is conditional computation: instead of running one big feed-forward block for every token, you keep many feed-forward blocks (“experts”) and use a router to pick a small subset per token.

It can feel like an ensemble, but the core idea is that you route each token to a few experts and only execute those experts.

MoE ideas date back to early 1990s work on “mixtures of local experts”. The modern resurgence for large-scale deep nets was popularized by Google’s sparsely-gated MoE layer (Shazeer et al., 2017).

Routing is usually implemented by scoring experts (often via softmax), selecting top‑k experts per token, and adding some form of load balancing during training so the router doesn’t collapse onto a single expert.

Core components

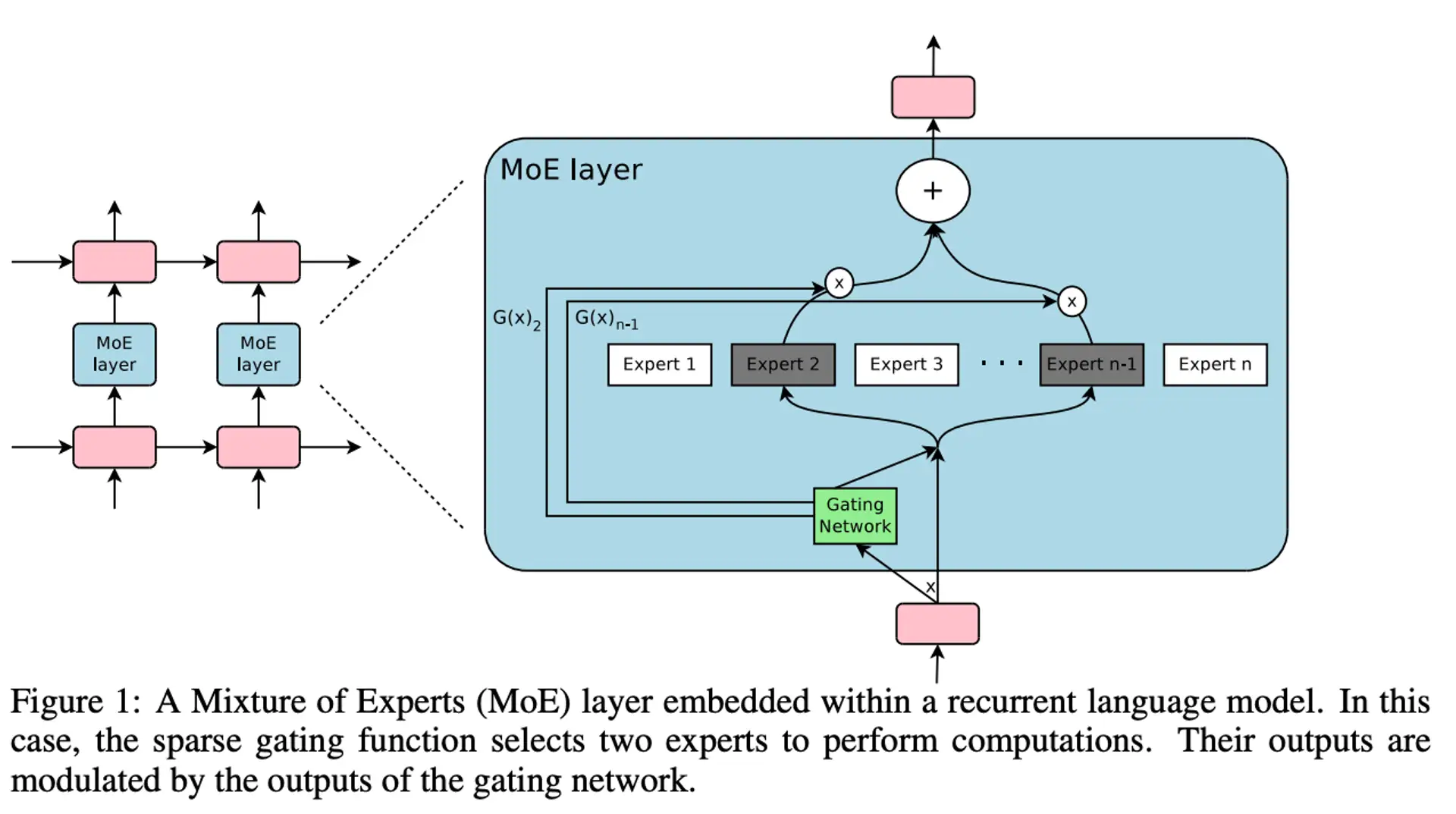
Illustration of a mixture-of-experts (MoE) layer. Only 2 out of experts are selected and activated by the gating network

Image source: Shazeer et al., 2017

Experts are multiple feed-forward sub-networks (separate weights), usually trained jointly. Specialization emerges because the router repeatedly sends similar tokens to similar experts.

The gating/router network scores experts for each token, selects the top‑k experts, and assigns combination weights. Training usually includes load balancing so routing doesn’t collapse onto one expert.

In a Transformer decoder block, the attention part stays the same; the MLP/FFN becomes an MoE. Roughly:

scores = router(h)              # one score per expert
ids = topk(scores, k)           # e.g., k = 2 for Mixtral
weights = softmax(scores[ids])  # normalize over selected experts
y = sum_i weights[i] * expert[ids[i]](h)

Costs and constraints

Where MoE fits

MoE tends to pay off when you can shard experts across multiple devices and you care about FLOPs per token at a given quality level. For single-device local inference, the “all experts in memory” requirement often makes dense models the simpler default.

Key takeaways

Sources and further reading

  1. Fedus, W., et al. (2021). “Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity.” arXiv preprint arXiv:2101.03961. Link

  2. Zoph, B., et al. (2022). “Designing Effective Sparse Expert Models.” arXiv preprint arXiv:2202.08906v1. Link

  3. Du, N., et al. (2021). “GLaM: Efficient Scaling of Language Models with Mixture-of-Experts”. Link

  4. Shazeer, N., et al. (2017). “Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer.” arXiv preprint arXiv:1701.06538. Link

  5. Bengio, Y., et al. (2013). “Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation.” Link

  6. https://huggingface.co/blog/moe

  7. https://www.artfintel.com/p/papers-ive-read-this-week-mixture?nthPub=201

  8. https://www.artfintel.com/p/more-on-mixture-of-experts-models

  9. https://lilianweng.github.io/posts/2021-09-25-train-large/#mixture-of-experts-moe

  10. https://www.youtube.com/playlist?list=PLvtrkEledFjoTA9cYo_wX6aG2WT5RFBY9

  11. https://www.youtube.com/watch?v=ccBMRryxGog&t=1038s